基礎知識
1.軌道要素

軌道とは、ある中心体の周りを周回する閉じた「道」です。ここでは、便宜上このような周回の中心を中心天体と表現します。

地球周回衛星とその軌道

一般的には、万有引力の法則により質量をもつあらゆるものが引き合っているので、天体だけではなくいかなる物体も中心体となりえます。もっとも、地球上では地球の重力が大きすぎてそのような力の影響を感じることはありません。地球の重力がキャンセルされている国際宇宙ステーションでは、地球上ではできないような実験が行われています。（周回の動画は4分から）

では、このように中心天体を周回せず、その場にとどまったらどうなるでしょうか？
周回運動を行っている物体が仮にその場に停止してしまった場合、重力に引っ張られて落ちてしまいます。つまり地球を周回している衛星も、太陽の周りをまわってる惑星たちも、中心に引っ張られて落ちないように必死に周回しているのです。その努力の成果が軌道となるのです。

軌道とは、前章で説明した通り中心天体を周回する物体の通過する道です。宇宙空間の中で衛星の位置を知るためには、航行する軌道がどのような形状で、特定の時刻に軌道上のどこにいるのかを求めなければなりません。まずは、軌道運動について勉強してみましょう。

17世紀ヨハネス・ケプラーは太陽系の惑星運動について研究し、その運動に関する3つの法則を導きました。

第1法則：「惑星は太陽を一つの焦点とする楕円軌道上を動く」
第2法則：「惑星と太陽を結ぶ線分が単位時間に描く面積は一定である」
第3法則：「惑星の軌道周期の2乗は太陽からの平均距離の3乗に比例する」

ケプラーの研究成果は惑星を衛星、太陽を地球と読み替えることで、地球周回衛星の軌道運動にもそのまま当てはまります。

ケプラーの第2法則：Area A = Area B = Area C
実際の面積は地球中心を起点とする扇形状

このような楕円形状および楕円上の位置は次のように6つのパラメータで表現できます。

１．軌道長半径：Semi-major Axis (a)

楕円軌道と軌道長半径

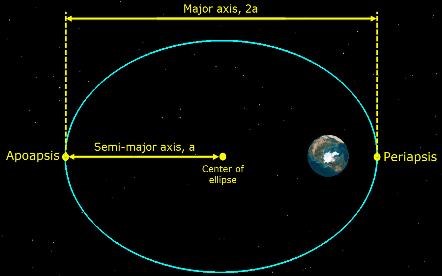
楕円長手方向の半径を軌道長半径と定めます。また、長手方向の直線をApse lineと呼び、動直線上に存在する中心天体に最も近い点を「近点」、最も遠い点を「遠点」と表現します。従って、中心から近点までの距離をr_p、同様遠点までの距離をr_aとしたとき、軌道長半径は次のように計算されます。

a = (r_p + r_a)/2

２．軌道離心率：Eccentricity (e)

軌道長半径と同様、楕円短手方向の半径をSemi-minor axis (b) としたとき、軌道離心率は次のように計算されます。

e = √(1-b²/a²)

あるいは近点距離、遠点距離を使用して次のように求めることもできます。

e = (r_a – r_p)/(r_a + r_p)

以上の式より、楕円軌道の特別な形態「円軌道は」近点距離と遠点距離が等しいので、離心率はe = 0となります。

軌道離心率と軌道の形状

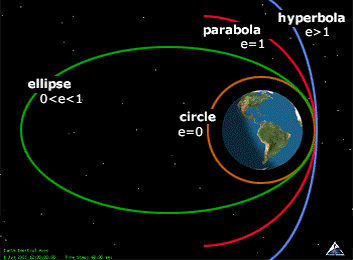
３．軌道傾斜角：Inclination (i)

軌道傾斜角とは、基準面（主に地球赤道面）と軌道面のなす角度です。基準面に対する軌道の傾きを示し、3次元の軌道を表現します。

異なる軌道傾斜角と地上航跡

上の動画は各軌道傾斜角における軌道の3次元表示と地上航跡を示しています。また、軌道傾斜角は地上航跡で表現した際の最大・最小緯度に一致しますので、衛星の地上航跡を観測することによって判断することができます。

軌道傾斜角が90度のケースは「極軌道」と呼ばれ、すべての緯度をカバーする特殊な軌道として知られています。

４．昇交点赤経：Right Ascension of Ascending Node（RAAN, Ω）

昇交点赤経とは、春分点の方向と軌道が赤道面を南から北へ通過する交点（昇交点）のなす角です。軌道傾斜角により定められた傾いた軌道面がどちらの方向を向いているのか決定するパラメーターとなります。

５．近点引数：Argument of Periapsis（AP, ω）（近地点引数：Argument of Perigee）

近点引数とは、昇交点と近点のなす角です。軌道傾斜角と昇交点赤経により定められた軌道面内で楕円がどちらの方向を向いているのか決定するパラメータです。そのため、同値が0-180度のときは近点は北半球、180-360度のときは南半球に存在することを示します。

また、特に地球周回の場合に近地点を表すPerigeeを使い、Argument of perigeeと呼ばれます。

６．真近点離角：True Anomaly（TA, ν）

真近点離角は１～５により決定された軌道上のどこに位置するのかを決定するパラメータです。近点上を0度とし、円1周360度の定義域を持ちます。

真近点離角の変化

～軌道要素まとめ～

STKを使用すれば、上記で説明した軌道要素を自由に変更して頂けます。
軌道要素に関する理解を深めるにはSTKは有効なツールの一つです。

それでは、ここまでの解説を基に次の問題を考えてみましょう。

問題

１．近地点は地球に最も近い軌道上の点を示す（〇 or ×）
２．円軌道の遠地点高度は、近地点高度の2倍である（〇 or ×）
３．昇交点赤経は人工衛星が本子午線を横切る地点から定義される（〇 or ×）
４．ケプラーの法則に基づく軌道要素は、いくつのパラメータで構成されていますか。またそれらの名前を答えなさい
５．真円の軌道離心率の値を答えなさい
６．衛星の軌道全体において絶えず変化する軌道要素を答えなさい
７．極冠（北極、南極行きの氷）を監視するために写真を撮るように設定された衛星の軌道傾斜角は、どのような値に近いか答えなさい

回答

１．〇　近地点は地球に最も近い軌道上の点です
２．×　円軌道では近地点と遠地点で同一の高度となります
３．×　昇交点赤経は春分点方向から定義されます
４．軌道長半径、軌道離心率、軌道傾斜角、昇交点赤経、近点引数、真近点離角の6つで構成されます
５．離心率はゼロです
６．絶えず変化する要素は真近点離角です
７．軌道傾斜角は90度に近い値となります

このように軌道要素を知ることは、衛星が現在どこにいて・どこに行くのか、つまり空間情報を手にすることになります。では、「どこにいる」というのは何を基準にしているのでしょうか。右や左、上下の概念のない宇宙空間で基準を設定することは共通認識を持つうえで不可欠な要素です。

次回は軌道要素の基準となるもの「基準座標系」について解説します。